Número de Fibonacci Na matemática, os Números de
Na matemática, os Números de Fibonacci são uma sequência (sucessão, em Portugal) definida como recurva pela fórmula abaixo:
Na prática: começa-se com 0 e 1, e então produz o próximo número de Fibonacci somando os dois anteriores para formar o próximo. Os primeiros Números de Fibonacci (sequência A000045 em OEIS) para n = 0, 1,... São
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946...
Uma grade preenchida com quadrados cujos lados são números de Fibonacci, formando sucessivamente rectângulos cada vez maiores e tendentes à razão áurea
Origens
Esta sequência foi descrita primeiramente por Leonardo de Pisa, também conhecido como Fibonacci (c. 1200), para descrever o crescimento de uma população de coelhos. Os números descrevem o número de casais em uma população de coelhos depois de n meses se for suposto que:
- No primeiro mês nasce apenas um casal,
- Casais amadurecem sexualmente (e reproduzem-se) apenas após o segundo mês de vida,
- Não há problemas genéticos no cruzamento consanguíneo,
- Todos os meses, cada casal fértil dá a luz a um novo casal, e
- Os coelhos nunca morrem.
A fórmula acima aplica-se ao problema dos coelhos porque se no mês n existirem A coelhos, e no mês n + 1 existirem B coelhos, então no mês n + 2 existirão, necessariamente, A + B coelhos. Isto acontece porque é sabido que cada coelho basicamente dá a luz a outro coelho todos os meses (na verdade, cada casal dá a luz a outro casal, mas é a mesma coisa), e isto significa que todos os A coelhos darão a luz a outro número de A coelhos que se tornarão férteis depois de dois meses, que é exactamente o mês n + 2. Então, no mês n + 2, existirá a população do momento n + 1 (que é B) mais a população no momento n (que é A).
O termo sequência de Fibonacci é também aplicado mais genericamente a qualquer função g onde g(n + 2) = g(n) + g(n + 1). Estas funções são precisamente as de formato g(n) = aF(n) + bF(n + 1) para alguns números a e b, então as sequências de Fibonacci formam um espaço vectorial com as funções F(n) e F(n + 1) como base.
Em particular, a sequência de Fibonacci com F(1) = 1 e F(2) = 3 é conhecida como os números de Lucas. A importância dos números de Lucas L(n) reside no fato deles gerarem a Proporção áurea para as enésimas potências:
L(n) = F(n - 1) + F(n + 1)
Fórmula explicita
Conforme mencionado por Johannes Kepler, a taxa de crescimento dos números de Fibonacci, que é F (n + 1) /F (n), tende à Proporção áurea, denominada φ. Esta é a raiz positiva da equação de segundo grau x2 − x − 1 = 0, então φ2 = φ + 1. Se multiplicarmos ambos os lados por φn, teremos φn+2 = φn+1 + φn, então a função φn é uma sequência de Fibonacci. É possível demonstrar que a raiz negativa da mesma equação, 1 − φ, tem as mesmas propriedades, então as duas funções φn e (1 − φ)n formam outra base para o espaço.
Ajustando os coeficientes para obter os valores iniciais adequados F (0) = 0 e F (1) = 1, temos
Quando n tende a infinito, o segundo termo tende a zero, e os números de Fibonacci tendem à exponencial φn/√5. O segundo termo já começa pequeno o suficiente para que os números de Fibonacci possam ser obtidos usando somente o primeiro termo arredondado para o inteiro mais próximo.
http://pt.wikipedia.org/wiki/Seq%C3%BC%C3%AAncia_de_Fibonacci
Grupo 06
Joana
Madalena
Teresa


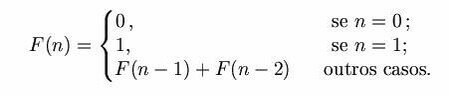


/https%3A%2F%2Fassets.over-blog.com%2Ft%2Fcedistic%2Fcamera.png)
/https%3A%2F%2Fprofilepics.canalblog.com%2Fprofilepics%2F3%2F1%2F315677.jpg)